Some Examples on MATLAB Symbolic Processing

Contents

Example 1: Solution of Ordinary Differential Equations

اكتب شفرة MATLAB لحل المعادلة التفاضلية الاتية:

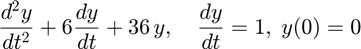
$$\frac{d^2y}{dt^2} + 6 \frac{dy}{dt} + 36 \, y ,\quad \frac{dy}{dt} = 1,\; y(0)=0$$

بين كيف يمكن رسم الحل الناتج في الفترة [0,3] بخطوة 0.01 

syms t
z = dsolve('D2y+6*Dy+36*y=0','y(0)=1','Dy(0)=0')

tm=0:0.01:3;
f=subs(z,t,tm);

plot(tm,f);
xlabel('t');
ylabel('y(t)');

 
z =
 
exp(-3*t)*cos(3*3^(1/2)*t) + (3^(1/2)*exp(-3*t)*sin(3*3^(1/2)*t))/3

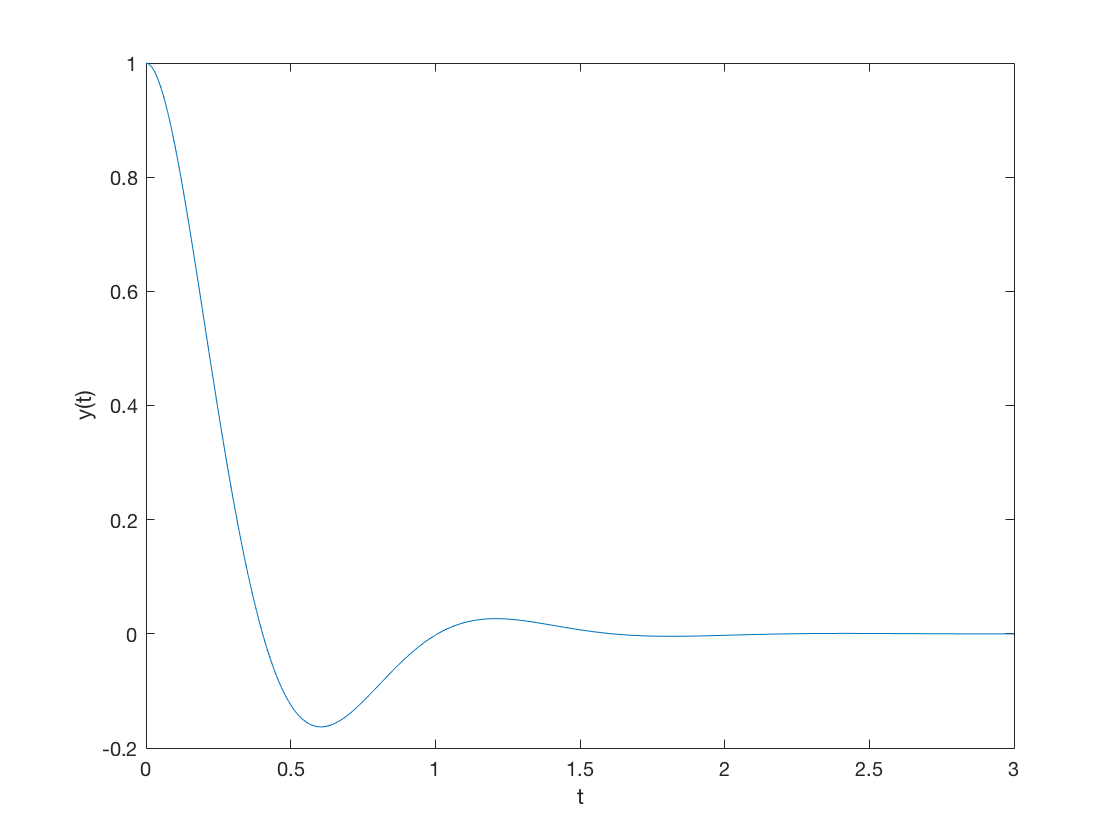
Example 1: Solution of Ordinary Differential Equations (Another Solution) 

syms t
z = dsolve('D2y+6*Dy+36*y=0','y(0)=1','Dy(0)=0',t);

tm=0:0.01:3;
for k=1:length(tm)
	f(k)=subs(z,t,tm(k));
end

plot(tm,f);
xlabel('t');
ylabel('y(t)');

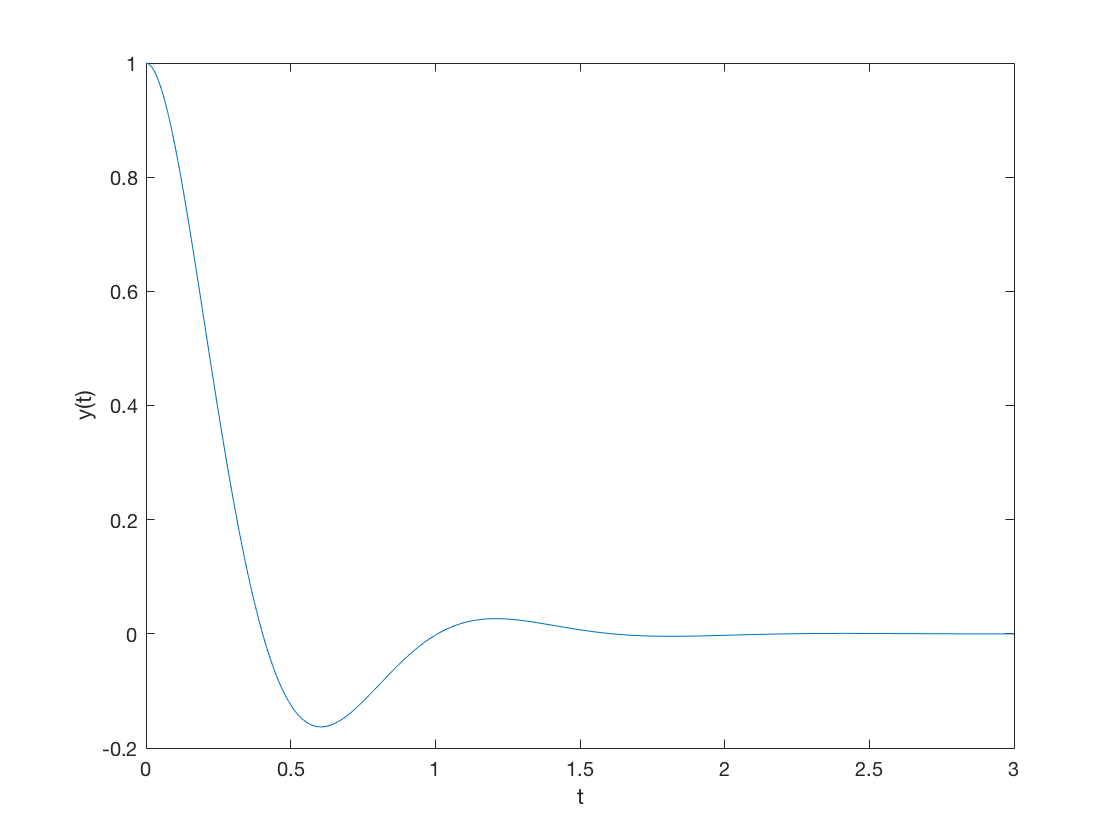
Example 2: Curve Intersection

Intersection of a line with a circle or ellipse إيجاد نقط تقاطع خط مستقيم مع دائرة او قطع ناقص

مثلا

$$\frac{x^2}{16} + \frac{y^2}{9} =1, \quad y=2\,x$$

الطريقة الاولي: باستخدام امر solve

تكون أوامر MATLAB كما يلي 

syms x y
eq1= x^2/16+y^2/9-1;
eq2=y-2*x;
s=solve(eq1,eq2);
x= s.x
y= s.y

 احداثيات نقط التقاطع
 
x =
 
 -(12*73^(1/2))/73
  (12*73^(1/2))/73
 
 
y =
 
 -(24*73^(1/2))/73
  (24*73^(1/2))/73

Example 2: Curve Intersection (Another Solution) الطريقة الثانية:

بالتعويض عن y في eq1 بدلالة x (من eq2) ثم إيجاد جذور متعددة الحدود الناتجة وتمثل الاحداثيات x لنقاط التقاطع ثم التعويض في y لإيجاد الاحداثيات y.
وعليه تكون أوامر MATLABكما يلي: 

syms x y z
eq1= x^2/16+y^2/9-1;
eq2=y-2*x;
polx=subs(eq1,y,2*x);
r=sym2poly(polx)  لإيجاد متعدد الحدود
x=roots(r)
y=subs(2*z,z,x)

r =

	0.5069         0   -1.0000


x =

	1.4045
   -1.4045

 
y =
 
  (24*73^(1/2))/73
 -(24*73^(1/2))/73


Author: Prof.Dr.Ing. Mohammed Nour AbdelGwad Ahmed | mnahmed@eng.zu.edu.eg
Computer and Systems Engineering Dept. | Faculty of Engineering | Zagazig University | Egypt
®2017 design and content: [(CC) BY NC SA] | run on MATLAB® R2016b